Tutorials: Electronics fundamentals (ELEFU)

Alternating Current AC

last updated: 2022-01-30

Quick links

Introduction
Why sinus and why 50Hz?
Characteristics of an AC voltage
Waveform
Dangerous current

Introduction

Song of this chapter: All songs by AC/DC ;)

Let's do a little history.

In 1887 in the United States Thomas Edison had constructed 121 DC power stations. At that time DC could not be easily converted to high voltages, needed to transport energy over longer distances. Edison promoted a system of many small, local power plants, that would power individual neighborhoods or city sections. With 110 V DC the voltage drop limited the maximum distance from the plant to the end user to 1.6 km. This limitation made power distribution in rural areas impossible.

In 1886 all Rome was electrified with AC. George Westinghouse ( entrepreneur and engineer from Pittsburgh) became aware of the new European alternating current systems in 1885 when reading an UK technical journal Engineering. He imported transformers and an AC electric generator, and began experimenting with AC networks and helped installing the first multiple-voltage AC power system. An hydroelectric generator produced 500 V AC stepped down to 100 V to light incandescent bulbs. The Westinghouse company installed more AC-lighting systems and by the end of 1887 it had 68 alternating current power stations.

The competition with Edison became the "War of the currents" with Thomas Edison spreading public perception that the high voltages used in AC distribution were unsafe.

"Just do (read and watch) it" AC1:

Read the wiki about the "war of the currents" and search for a documentary on youtube.
A Luxembourg engineer, inventor, and industrialist developed the first commercially usable lead-acid battery (1882) and electrified the first town in Luxembourg on 24 October 1886! Research his name and the town that was electrified!

Why sinus and why 50Hz?

Most power plants (water, wind, coal, nuclear, gas) give us mechanical (kinetic) energy of rotation (from steam turbines, gas turbines or water turbines). With generators (dynamos or alternators) this rotational energy is converted to electrical energy.

A current (moving electrons) produces a magnetic field. Bending a wire into multiple closely spaced loops to form a coil gives us an electromagnet.

Electromagnetic induction

On the other hand a moving wire (or a coil) in a magnetic field produces a voltage. This is called electromagnetic induction. A conductor loop (or a coil of wire) rotating in a magnetic field produces a current which changes direction with each 180° rotation, an alternating current (AC).

The inducted voltage u depends on the changing of the magnetic flux Φ per time and the number of windings (N) of the coil.

The magnetic flux depends on the magnetic flux density B of the magnetic field and the effective area of the conductor loop A in the magnetic field.

The width w of the effective loop area in the magnetic field is maximum at 0°, and zero at 90°. It can be calculated with the cosine (cos) of the angle α.

The changes of the magnetic flux is minimal at 0° and 180° and is biggest at 90° (negative) and 270°. The derivative of a cosine gives a sinus.

That's why sinus :).

Induced voltage u

The induced voltage u can be calculated with the help of the sine function:

"Just do (watch) it" AC2:

Search for the video "How generator works by Khurram Tanvir" and watch it.

Characteristics of an AC voltage

Here is the oscilloscope screen of a measured voltage in a wall socket. The oscilloscope measured three voltages, the frequency and the period. Let's take a closer look at these physical quantities.

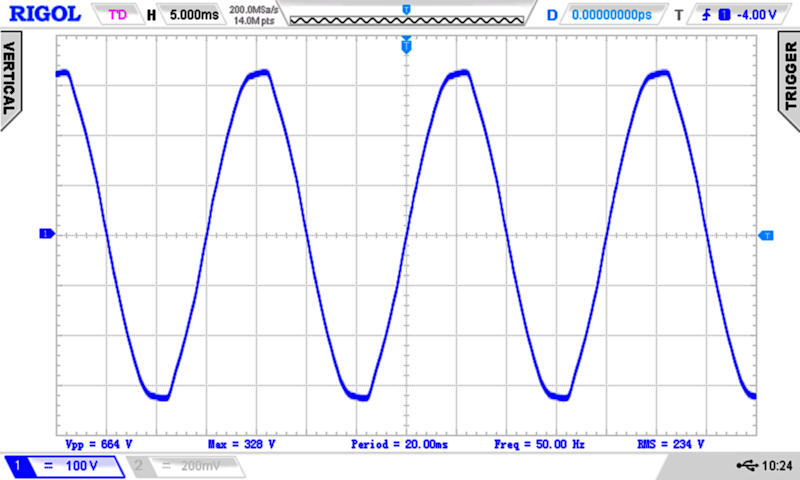
Peak voltage `û` and peak to peak voltage `U_SS`

û (U_s, V_p) is the peak voltage in Volt (V).

On the oscilloscope screen it is named Max.

This voltage in the European power supply system is 325 V.

The peak-to-peak voltage of an AC voltage U_SS (V_pp) in Volt (V) is the difference between its positive peak and its negative peak. For a sinusoidal voltage (sin(x) goes from +1 to −1) the maximum values swing between +û and −û.

The peak-to-peak voltage is therefore û−(−û) = 2û.

Period `T`, frequency `f` and angular frequency `ω`

The amplitude of the voltage is changing in the rhythm of the sine between the peak values. One period is one revolution of the generator (0 - 360°).

The time needed for such a revolution depends of the rotating speed of the generator. If the generator turns with 3000 revolutions per minute or 50 revolutions per second we get 50 periods per second. One sine wave of the voltage returns 50 times in one second. This is called the frequency f of the voltage. The time needed for one period is called periodic time T.

Frequency is the number of occurrences of a repeating event per unit of time. The symbol is f and the unit is hertz Hz or s^-1 (cycle per second).

The period T is the duration of time of one cycle in a repeating event, so the period is the reciprocal of the frequency. It's unit is the second s.

One revolution is equal to 360° or 2π radians. We can use the angular frequency ω to connect the time of one revolution with the angle.

The angular frequency ω is a scalar measure of rotation rate. It's unit is radians per second (s^-1).

For our sine wave we get:

with the momentary angle:

So, why 50 Hz?

The alternating current needed a frequency high enough to avoid flickering (see following exercise in this chapter) and not too high for the rotational speed of the generators.

Effective voltage `U` (`U_eff`, `U_RMS`)

The peak voltage is not a good value to describe the effect of an AC voltage. We want an AC voltage value that has the same effect than a DC voltage (how hot gets a radiator or how bright is a lamp). To find this voltage we use the time averaged power of an AC voltage that equals the DC power with this voltage.

Instantaneous power p(t) can be calculated with:

A time averaged power P (where the averaging is performed over any integer number of cycles and with the same effect than DC power) can be calculated using this new AC voltage value called effective value U_eff (Europe) or root mean square value U_RMS (V_RMS) or simply a big U.

The effective voltage of a waveform can be calculated with the corresponding crest factor:

Sine wave (crestfactor = √2 = 1,4142):
Triangle wave and sawtooth wave (crestfactor = √3 = 1,732):
Square wave (crestfactor = 1):

"Just do it" AC3:

We want to measure the AC voltage in our socket. Because this is potentially :) dangerous, we will use a transformer to reduce the voltage and nevertheless be able to visualise the curve of the voltage. Read and copy the characteristics marked on the transformer.
We will use our multimeter to measure the AC voltage and the frequency of the voltage (frequency range). What maximum and minimum frequencies the used multimeter can measure (read the manual, look at the frequency range)? What maximum frequency the AC voltage may have to measure correct RMS values (AC voltage range)?
Measure and note the voltage(s) and frequency(ies) and compare them with the characteristic of the transformer. Why do we have a difference?
To view the voltage characteristic we will use an oscilloscope. We use a mixed-signal-oscilloscope from Rohde & Schwarz. The RTC 1002 has 2 channels and can display signals up to 100 MHz. Our oscilloscope is able to save the oscilloscope pictures to an USB-stick. You will use this feature to document this exercise and all future exercises where the oscilloscope is needed. Document the oscilloscope picture of the AC voltage.
Measure the period time, frequency and voltages (U_p, U_pp, U_RMS) with the oscilloscope. Calculate the root mean square and compare with your values from the voltmeter and the oscilloscope.
Comment the measured values and the measured waveform.

Waveform

Alternating voltages and currents can come in a number of different waveforms. With oscilloscopes we can see the changing amplitudes over time. The shape of these amplitudes often gives the name of the waveform:

Square waves are used for example in digital switching electronics, as timing references (clock signals) and in music synthesizers (square waves sound hollow, and are used as the basis for wind instrument sounds).
Triangle waves are also found in sound synthesis and are useful for testing linear electronics like amplifiers.
Sawtooth waves are often used in music synthesizers, in switched-mode power supplies and the sawtooth wave is used to produce vertical and horizontal deflection signals used to generate a raster on CRT-based television or monitor screens.
PWM waves have multiple applications, as servo control, encoding, voltage regulation and power delivery.

To produce different waveforms, we can use a function generator. These instruments are not meant to produce powerful signals with high currents like a power supply, but to produce waveforms to measure properties of circuits. They have an output resistance of 50 Ω.

"Just do it" AC4:

Reproduce the waveforms from above with the help of a two channel arbitrary waveform generator (1 µHz - 10 MHz) from PeakTech, the PeakTech 4124 or 4125 and your oscilloscope. Use both channels and document the 3 images (USB screenshots on your oscilloscope). Connect the function generator to a piezoelectric speaker and listen to the different wave-forms.
Lets use our ESP32 board to produce and measure alternating voltages (the chip is running with 3.3 V!). The first Arduino sketch will produce the simplest waveform, a square wave. This is done with the simple blink demo program. Connect an LED to digital pin 16 and test the following program. Calculate the period time T and the frequency f. Watch the signal on the oscilloscope and measure T and f with the oscilloscope. Save in all following exercises the oscilloscope pictures to an USB-stick and use them to properly document your tasks.
```
  // iot_jdi_AC4.ino (blink)
  // weigu.lu

  const byte PIN_SQUARE_OUT = 16;
  unsigned int delay_time = 100;

  void setup() {
    pinMode (PIN_SQUARE_OUT, OUTPUT);
  }

  void loop() {
    digitalWrite(PIN_SQUARE_OUT, LOW);
    delay(delay_time);
    digitalWrite(PIN_SQUARE_OUT, HIGH);
    delay(delay_time);
  }
```
Reduce the delay time until you can't see the blinking no more. Calculate the frequency. If you are interested in this phenomena read the wiki articles about the flicker fusion threshold and the persistence of vision.
Now we replace the LED with a piezoelectric speaker. Replace the delay() function with the delayMicroseconds() function. Calculate the different values for delay_time, so we can hear tones of 200 Hz, 1 kHz and 10 kHz.
Comment the two delay lines with // and measure the maximal frequency the ESP32 can deliver. The square is no more symmetric because the ESP32 has an operating system running in the background and that consumes time.

"Just do it" AC5:

With the next sketch we create a pulse-width modulation (PWM). The frequency of the square stays the same, but the square will not stay symmetric (pulse width time + off-time = constant). To change the width of the pulse we connect the wiper of a 10 kΩ potentiometer to pin 4. The other two terminals go to 3.3 V and GND. We use the monitor to view the potentiometer values. Test the following sketch (oscilloscope and speaker connected). Document the oscilloscope screen for a pulse width of about 80% of the period:

  // iot_jdi_AC5.ino
  // weigu.lu

  const byte PIN_SQUARE_OUT = 16;
  const byte PIN_POTENTIOMETER = 4;

  unsigned int delay_time = 4095;
  unsigned int pulsewidth;

  void setup() {
    Serial.begin(115200);
    pinMode (PIN_SQUARE_OUT, OUTPUT);    
  }

  void loop() {
    pulsewidth = analogRead(PIN_POTENTIOMETER); 
    Serial.println(pulsewidth);
    digitalWrite(PIN_SQUARE_OUT, LOW);
    delayMicroseconds(delay_time - pulsewidth);
    digitalWrite(PIN_SQUARE_OUT, HIGH);
    delayMicroseconds(pulsewidth);
  }

Write in your words the definition of duty cycle (wiki). Find the formula to calculate the duty cycle. Draw an U = f(t) diagram for a duty cycle of 30 % by hand. Mark t_i, t_p and T in the diagram.
Connect an LED instead of a speaker. Calculate the pulse-width value needed for a duty cycle of 30 %. Eliminate the potentiometer and serial code to get an accurate result and document the oscilloscope screen.

"Just do it" AC6:

The ESP32 has two internal Digital-to-Analog Converters (DAC). These are faster than PWM. We can use our ESP32 to build a function generator that produces different wave-forms. Here is an example. Analyze the program and document it. Read the following article about Arduino arrays. Why don't we calculate the array during the main loop?
Test the program:

  // iot_jdi_AC6.ino
  // weigu.lu
  // DAC1 on IO25, DAC2 on IO26 (8 bit)

  float y = 0; 
  byte sine[255];    
  byte i = 0;

  void setup() {
    for (i=0; i<255; i++) {         
      y = sin(((float)i/255)*2*PI); 
      sine[i] = byte(y*128)+128; 
    }
  } 

  void loop() {
    for (int i=0; i<255; i++) { 
      dacWrite(DAC1, sine[i]);
      dacWrite(DAC2, 255-i);
      delayMicroseconds(1); 
    }
  }

Oscilloscope the voltages on DAC1 and DAC2. What is the name of the second waveform?
Change dacWrite(DAC2,i); to dacWrite(DAC2,255-i);. Comment the result.

Fourier_series

As seen the most common type of AC is the sine wave.

The french mathematician Joseph Fourier discovered in 1822 that the sine wave has a very special characteristic.

Any periodic waveform can be described with a sum of sine (or/and cosine) waves.

The study of the way functions may be represented or approximated by sums of e.g sine waves is called Fourier analysis. The representation of a function as the sum of simple sine waves is called a Fourier series.

"Just do it" AC7:

The following program visualizes the synthesis of a square wave by adding sinuses. Connect the two channels of your oscilloscope to DAC1 and DAC2 of your ESP32.
As you see we add the harmonics with 3f, 5f, 7f and 9f with a reduced amplitude of 1/3, 1/5, 1/7 and 1/9. Test the program and document all the screens.

  // iot_jdi_AC7.ino
  // weigu.lu
  // DAC1 on IO25, DAC2 on IO26 (8 bit)

  const byte Y_MAX = 80;
  byte i = 0;
  unsigned int j = 0;
  float y = 0; 
  byte sine[255],sine3[255],sine5[255],sine7[255],sine9[255];

  void setup() {
    for (i=0; i<255; i++) {         
      y = sin(((float)i/255)*2*PI); 
      sine[i] = byte(y*Y_MAX); 
    }
    for (i=0; i<255; i++) {         
      y = sin(((float)i/255)*2*3*PI); 
      sine3[i] = byte(y*Y_MAX/3); 
    }
    for (i=0; i<255; i++) {         
      y = sin(((float)i/255)*2*5*PI); 
      sine5[i] = byte(y*Y_MAX/5); 
    }
    for (i=0; i<255; i++) {         
      y = sin(((float)i/255)*2*7*PI); 
      sine7[i] = byte(y*Y_MAX/7); 
    }
    for (i=0; i<255; i++) {         
      y = sin(((float)i/255)*2*9*PI); 
      sine9[i] = byte(y*Y_MAX/9); 
    }
  } 

  void loop() {
    for (j=0; j<1000; j++) { 
      for (i=0; i<255; i++) { 
        dacWrite(DAC1, sine[i]+128);  
        dacWrite(DAC2, sine3[i]+128); 
        delayMicroseconds(1); 
      }
    }
    for (j=0; j<1000; j++) { 
      for (i=0; i<255; i++) { 
        dacWrite(DAC1, sine5[i]+128);  
        dacWrite(DAC2, sine7[i]+128); 
        delayMicroseconds(1); 
      }
    }
    for (j=0; j<1000; j++) { 
      for (i=0; i<255; i++) {       
        dacWrite(DAC1, sine[i]+sine3[i]+128); 
        dacWrite(DAC2, sine[i]+sine3[i]+sine5[i]+128); 
        delayMicroseconds(1); 
      }
    }  
    for (j=0; j<1000; j++) { 
      for (i=0; i<255; i++) {       
        dacWrite(DAC1, sine[i]+sine3[i]+sine5[i]+sine7[i]+128); 
        dacWrite(DAC2, sine[i]+sine3[i]+sine5[i]+sine7[i]+sine9[i]+128); 
        delayMicroseconds(1); 
      }
    }
  }

Change the harmonics to 2f, 3f, 4f and 5f with a reduced amplitude of 1/2, 1/3, 1/4 and 1/5. Which wave-form will arise? Document the screens.

Let's have a closer look on the Fourier series of a square wave:

We see that a square wave with a certain base frequency f can be created by adding to a sine wave with the same base frequency and an amplitude of 4/π = 1.2732 to a second sine wave with 3 times the base frequency and an amplitude of 4/3π = 1.2732/3 and a third sine wave with 3 times the base frequency and an amplitude of 4/5π = 1.2732/5 and so forth.

Harmonics of a wave with a base frequency f are waves with a frequency that is a positive integer multiple of the frequency f. So the original wave is also called the 1st harmonic. All other waves with a multiple of f are named higher harmonics. For example, if the fundamental frequency is 220 Hz (note a (la) in music), the frequencies of next three higher harmonics are 440 Hz (2nd harmonic, also an a (la) in music but an octave higher), 660 Hz (3rd harmonic) and 880 Hz (4th harmonic, also a (la) in music but 2 octaves higher). The differences of sound in music instruments playing the same note (base or fundamental frequency) are the mixture of the higher harmonics. Listen to the "additive square demo" on wikipedia.org/wiki/Square_wave. Take also a look at the "Animation of the additive synthesis of a square wave with an increasing number of harmonics".

Even by adding multiple sine waves up to very high frequencies, the square wave is not perfect! There will always be little ripples (ringing artifacts) and the rise time (time to change from a low to high) will not be infinite low.

This tells us a very important lesson.

It is impossible to achieve in physical systems an ideal square wave (instantaneously changes between the high and the low state and no under- or over-shooting). This would require an infinitebandwidth, but every real system has the characteristic of a low-pass filter. To transport a digital signal, the passing frequency of the used transportation channel must be much higher than the base frequency of the signal.

We will take a closer look to low-pass filter in the next chapter.

If we use an oscilloscope of 20 MHz to watch a perfect digital signal of 10 MHz, we will see a sine wave!! Even with an oscilloscope of 100 MHz we will not see the real signal!

Another example:
In older days :) the telephone line was limited to 3.4 kHz. It was not possible to pass a digital signal directly at a reasonable high frequency. So it was necessary to use a modem (modulator-demodulator). Instead of sending a digital signal four sine waves were used. The call originator used sine waves at 1070 Hz and 1270 Hz (for low and high) and the answering modem 2025 Hz and 2225 Hz. This modulation is a frequency modulation and is called Frequency-shift keying (FSK) and allowed full-duplex at 300 bit/s! (50 years ago). If you want to see modem with acoustic coupler watch the film war games from 1983.

Square waves, often used in digital circuits, contain a wide range of harmonics. These can generate electromagnetic radiation that interferes with other nearby circuits, causing noise or errors. An enclosure of a conductive material (normally metal) called a Faraday cage can prevent electromagnetic interference.

Any signal that can be represented as a variable that varies in time has a corresponding frequency spectrum. On the following picture we see the frequency spectrum of three different waveform's:

"Just do it" AC8:

Our oscilloscope has the possibility to watch the frequency domain with a fast Fourier transform function FFT (read the manual). Use the frequency generator with a square wave and a frequency of 500 kHz and document the screen. Determine the amplitudes of the first, third and fifth harmonic of the square wave in decibel-milliwatts dbm and in Volt V.
What are dbm? Search the net and explain. How many watt (W) are 20 dBm, -30 dBm and -90d Bm? Use the corresponding formula.
Calculate the voltages from the dBm values of your measured first, third and fifth harmonic. The resistance of your frequency generator is 50 Ω.

Electromagnetic spectrum (wiki)

Class	Denomination	Short	Frequency	Wavelength
-------------------------	------------------------	-----	---------	---------
	Gamma rays	γ	300 EHz 30 EHz	1 pm 10 pm
Ionizing radiation	Hard X-rays	HX	300 EHz	1 pm
	Soft X-rays	SX	300 PHz	1 nm
	Extreme ultraviolet	EUV	30 PHz 3 PHz	10 nm 100 nm
-------------------------	------------------------	-----	---------	---------
Visible radiation =>	Near ultraviolet	NUV	3 PHz 300 THz	100 nm 1 µm
	Near infrared	NIR	30 THz	10 µm
	Mid infrared	MIR	3 THz	100 µm
	Far infrared	FIR	300 GHz	1 mm
-------------------------	------------------------	-----	---------	---------
	Extremely high frequency	EHF	300 GHz 30 GHz	1 mm 1 cm
Microwaves	Super high frequency	SHF	3 GHz	1 dm
	Ultra high frequency	UHF	300 MHz	1 m
	Very High frequency	VHF	30 MHz	10 m
and	------------------------	-----	---------	---------
	High frequency	HF	30 MHz 3 MHz	10 m 100 m
	Medium frequency	MF	300 kHz	1 km
	Low frequency	LF	30 kHz	10 km
Radio waves	Very low frequency	VLF	3 kHz	100 km
	------------------------	-----	---------	---------
	Ultra low frequency	ULF	3 kHz 300 Hz	100 km 1 Mm
	Super low frequency	SLF	30 Hz	10 Mm
	Extremly low frequency	ELF	3 Hz	100 Mm

Dangerous current

In the war of currents Edison used the danger of currents to argue against AC voltage. A pamphlet claimed DC had not caused a single death, and included newspaper stories of accidental electrocutions caused by alternating current. Westinghouse on the other side pointed out in letters to various newspapers the number of fires caused by DC equipment.

If you touch the electric wire around a meadow, you touch a voltage of 2000 V - 5000 V. Why does this high voltage does not kill you on the spot?

It's not the voltage that kills (voltage can hurt without direct damage), but the height of the current and the duration the current passes the heart. The current of the meadow wire is limited to 100 mA - 300 mA and the duration to 20 ms - 100 ms.

Effects of electrical current in the human body

The IEC publication 60479-1 defines four zones of current-magnitude /time-duration. In each of these four zones the physiological effects are described.

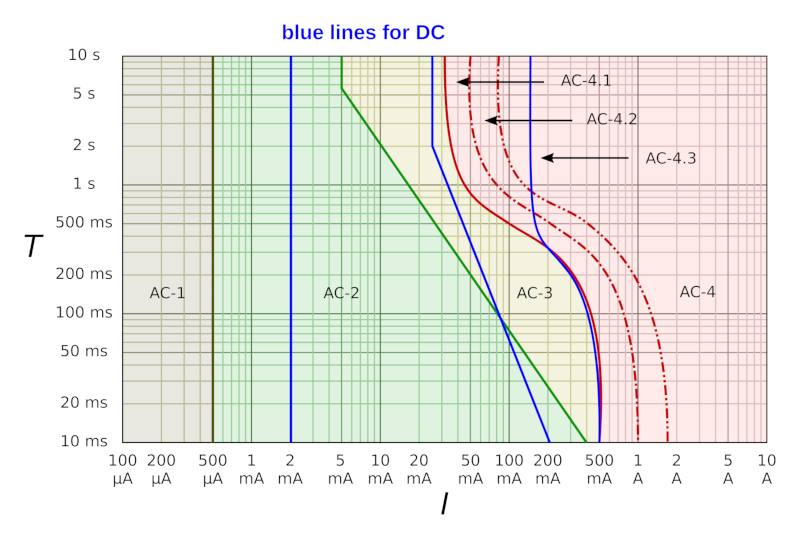
Source: Graphic by Cmglee under Creative Commons Attribution-ShareAlike 3.0 Unported license(CC BY-SA 3.0).

Time/current zones for AC 15 Hz to 100 Hz for hand to feet pathway

Zones	Boundaries	Physiological effects
AC-1	Up to 0.5 mA	Perception possible but usually no ‘startled’ reaction
AC-2	0.5 mA up to green curve	Perception and involuntary muscular contractions likely but usually no harmful electrical physiological effects
AC-3	Green curve up to red curve	Strong involuntary muscular contractions. Difficulty in breathing. Reversible disturbances of heart function. Immobilization may occur. Effects increasing with current magnitude. Usually no organic damage to be expected
AC-4 ₁₎	Above red curve	Patho-physiological effects may occur such as cardiac arrest, breathing arrest, and burns or other cellular damage. Probability of ventricular fibrillation increasing with current magnitude and time
	AC-4.1	Probability of ventricular fibrillation increasing up to about 5 %
	AC-4.2	Probability of ventricular fibrillation up to about 50 %
	AC-4.3	Probability of ventricular fibrillation above 50 %

₁₎
For duration's of current flow below 200 ms, ventricular fibrillation is only initiated within the vulnerable period if the relevant thresholds are surpassed. As regards ventricular fibrillation, this figure relates to the effects of current which flows in the path left hand to feet. For other current paths, the heart current factor has to be considered.

As we see above, the differences between AC and DC are not huge.

Simplified we could state that for a short time (less than 200 ms) a human can stand 50 mA (AC or DC).

Ohm's law states that the current drawn depends on the resistance of the body. Every person has his own resistance as a lot of different factors are involved (e.g. like for wires as resistors, the resistance of an arm or leg depends on it' length and diameter). Men tend to have lower resistance than women (thicker arms and legs). A rough value for the internal resistance of the human body is 300 Ω - 1000 Ω. The path that electricity takes through the body is also important (e.g. the resistance from hand to foot is bigger than the distance from thumb to ring-finger on the same hand).
But the main resistance comes from the skin, witch is a poor conductor if it's not wet or burnt/blistered. The resistance from dry skin is between 1000 Ω - 100000 Ω.

The total resistance is:

For simplification we will memorize that the total resistance of the human body is 1000 Ω.

"Just do (calculate) it" AC9:

Try to measure your resistance with the ohmmeter. Try also with wet hands. Do you think this measurements may be dangerous for you (argument)?
Calculate the maximum voltage you can touch without being in danger, if your resistance is 1000 Ω.

It is the current that kills, but anyway we can state:

Voltages above 50 V AC and above 120 V DC are dangerous!
For children and animals voltages above 25 V AC and above 60 V DC are dangerous!
Voltages under 25 V AC and under 60 V DC schould be used, they are not dangerous!

"Just do (research) it" AC10:

Currents above 200 mA, will produce severe burns and unconsciousness. Research the first aid actions that have to be taken in the case of an electric shock.

Other dangers

A current through a wire causes heat, and so a third of all fires is caused by short circuits or overheating of electric equipment. Other dangers of electricity are the high forces generated through magnetism at high currents, or flash burns of the eyes flash arcs caused in short circuits. A current through a fluid can also produce toxic or explosive gases.

Interesting links:

http://www.jezzamon.com/fourier/index.html